Morphogenesis of chords and scales / Chords and scales classification
(Llorenç Balsach, from the book "La convergència harmònica", Barcelona 1994, ISBN 84-85927-44-3, see summary in the article: Aplication of Virtual Pitch Theory in Music Analysis)
On pages 56-61 we have written up harmonic tables where are represented by order all (!) the chords and scales that could be formed with the 12-tone equal tempered system, classified according to their convergent sub-chords fundamentals. Scales and chords are grouped in accordance with the number of notes (numbers of different pitch classes) they have and in each group the order is established by their harmonic structure. (See also Separation of chords into convergent chords)
The notes pointed out are not scales and chords with their traditional musical meaning, but they are groups of notes representing a wide family of musical statements. Depending on the horizontal or vertical musical thought each group of notes could be considered as chords (even if they are written as scales) or arranged as scales (even if they are written as chords). It is only for reasons of clearity that the groups of up to six notes are printed as chords while those of seven note or more appear as scales.
We will see that at certain equivalence level between inversions and modes the number of chords and scales that could be formed is the same so they could have the same harmonic representative which is the one that appears in the chord-mode class tables.
Equivalence level between chords
In musical theory or analysis, to say that two chords or two scales are the same could have many different interpretations. Normally, one trusts the reader's own musical judgement to deduce the correct equivalence level of the two chords. On a more precise level, two chords are the same only if they are in the same octave, have the same notes and layout. On another level, two chords are equivalent if they have the same notes but this equivalence is only stated by the bass. Also, if one chord is the transposition of the other, if it is the inversion, and so forth.
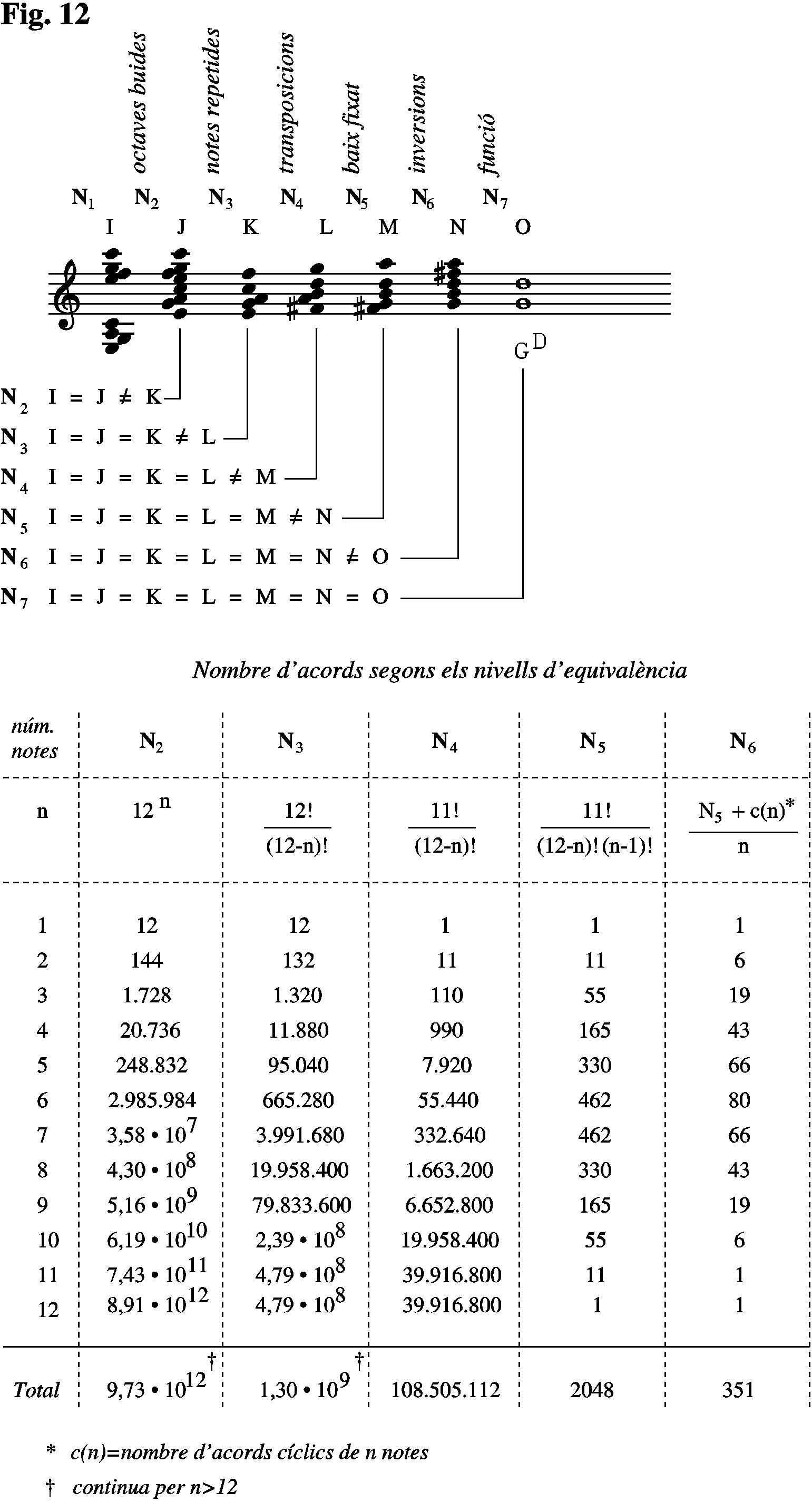
The different equivalence levels and the number of (different) possible chords in each equivalent group (each level includes the previous equivalence level) are shown in Fig. 12.
When working with the 12 tone closed equal tempered gamma a first equivalence already assumed and not specified in Fig. 12 is the enharmonic equivalence. That doesn't mean indifference when representing the same note in a way or another, on the contrary, following the thesis of our research, the convergence implies a precise harmonic notation.
On the N1 level, two chords are equivalent only if they are exactly the same; at this level, the total number of chords is not specified because it is almost unlimited.
On the N2 level, two chords are equivalent if they coincide with the removal of empty octaves or they strict transpositions of octave (of the whole chord). The number of possible chords in this group is still very wide (thousands of billions).
On the N3 level, the previous equivalence is included and the duplicated upper notes can be eliminated or upper octaves of individual notes added without affecting the chord's identity. The number of chords in this case is more that a thousand million (1.302.061.344 chords).
On the N4 level, the previous equivalences are included and two chords can be identified if one is the strict transposition of the other. The number of possible chords in this group is still very high (108.505.112 chords).

On the N5 level, the previous equivalences are included and two chords can be considered equivalent with any internal order of notes except for the bass. In this group we could include the triadic chords of traditional harmony and their inversions (as non-equivalent chords). The number of possible chords in this level is considerably reduced (2048).1
On the N6 level, the previous equivalences are included and two chords can be identified if one is the inversion of another one. In fact, at this level, a chord (also known as chord class) can be considered as a non-ordered collection of notes or, better to say as a collection of intervals (bearing in mind the N4 equivalence). The number of different chords is only 351 which are the ones represented on the chord-mode class tables.
Moreover, a N7 level could be considered, made up of the "chords" that constitute the fundamentals. The number of functional chords is not precise because on a certain level of complexity the chords can be decomposed into different convergent chords. For the majority of chords of up to five notes we could state that the number of wide functional types is reduced to seven (see fig.18).
Equivalence levels between scales
Before studying the scales we would like to explain the meaning of the concepts of scale, mode, scaling and gamma as interpretations of these terms can vary widely.
A gamma is every palette of notes or intervals (in fact, different systems of tuning), theoretical or practical, historical or contemporary, from different human cultures. This will be the case of the Pythagorean, Zarlinian, equal tempered... or any other system.
A scaling is only a cyclical succession of intervals (the beginning and end do not affect the identity of the scaling). For example, the white keys of a piano are a scaling and the black ones are another different scaling.
Mode is a scaling where a note (belonging to it) and the octave equivalence relation establish a cycle and a hierarchic relationship in the same scaling. So, a scaling will have as many different modes as different notes.2 In the scaling of the white keys in the piano, D for example, defines the intervalic cycle D-C (doric mode), F, the F-E (Lydian mode) and so on, establishing a hierarchic relation as it becomes a reference note in the cadencial processes.
Scale, in my opinion would be a mode associated with –transposed– into a precise tone (D minor scale, G doric scale, etc.) so every mode would have 12 scales, but because of the generalized use of the word scale to refer to any gamma, scaling, mode and in general, any horizontal succession of sounds we will continue to use the word scale in that generic use.
Transpositions do not modify the identity of the scalings or the modes (Fig. 13).
Working from this definition, the number of different modes is 2048 and the number of different scalings is 351 (!). So, the number of modes is the same as the number of chords in the equivalence level N5 and the number of scalings is the same as the number of chords in the level N6 (chord classes). This gives us enough arguments to think that there is an equivalence relationship between the concepts of chord inversion and the mode of a scale.

Chord-mode classes
The fact that the number of scalings can coincide with the number of chord classes in the equivalence level N6 is easy to explain. We will realize that a chord-class, thinking of this level of equivalence, has an only scaling and viceversa. We have only to order the chord-class horizontally according to the order established by the 12 tone chromatic scale to obtain a unique scaling –because level N6 is only a collection of notes without having any preference for a particular one–. That is to say, the chord becomes a representative of the scaling as it does not matter which is the first note of the collection of notes. The opposite process is easier to understand. For example, if we take out the black keys of the piano and put them in a bag, we have gone from a scaling to a chord class on level N6.
If we can eliminate this conceptual difference between chord class N6 (vertical group of notes) and scaling (horizontal note groupings), we will have defined that we understand by chord-mode class. To make it easy we could say that collections of notes (apparently different) belong to the same chord-mode class if they can be ordered or reduced to the same intervalic pattern. All the collections of notes that belong to a same chord-mode class have the same decomposition into convergent structures which at the same time define it. We could also say that a chord-mode class is formed by a chord with all its inversions and transpositions in any vertical or horizontal combination. In Fig. 13 we have a lot of chords and scales but only one chord-mode class, the one represented in the chord-mode tables on page 59 by number 2 in the seven notes chordal group and formed by two complete convergent chords at a distance of a minor seven. As we have said before, we have only 351 possible chord-mode classes.
We must not misunderstand our definition of chord-mode class with a very widely used term, the PC-Set (Pitch Class Set) introduced by M. Babbit and developed by A. Forte in his book The Structure of Atonal Music (1973). To Forte, two chords or scales are equivalent by inversion if there is an intervalic symmetry between both of them. So he uses the concept of intervalic inversion that is applied normally to scales and specially to serial music and which could be misunderstood with the term inversion of chords that appear in harmony treatises (which is, in fact, the one we are using). For Forte, the major triad (C:E:G) and the minor triad (C:Eb:G) are different manifestations of the same PC-Set represented by (0,3,7) or 3-11 (because they are equivalent by an inversion and a transposition). A similar equivalence occurs between the dominant seventh chord and the Tristan chord (PC-Set 4-27). From our functional point of view, these identifications are not acceptable for the analysis of the harmonical tensions, even if we are talking about atonal music. They can be very useful for the research or construction of geometrical-structural relationships4(specially in weak tonal areas) but major and minor triads have a different harmonic-functional meaning for the hearing system; the same happens with the dominant seventh chord and the Tristan chord.
The importance of a chord-mode class comes from the fact that it has, for all its inversion and mode family, only one decomposition into convergent chords. Knowing the potency of each convergent sub-chord, represented by the figure of the fundamentals, it is easier to study the harmonic tendencies of the chord-mode classes.
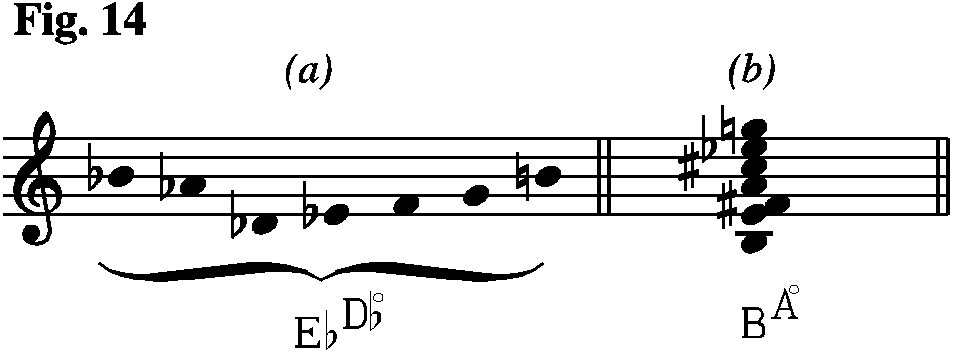
For example, the scale (a) in Fig. 14 (the same chord-mode class as in Fig. 13) has a tendency to resolve towards Ab or, in other words, Ab is its tonic because the fundamentals of this chord-mode class are precisely the dominant and the subdominant of Ab (enharmony Cb=B). But, at first sight, the scale could belong to C minor. In fact, this tendency to C exists but it is only as a secondary form as a 2nd. order homotonic resolution of the secondary fundamental, like the secondary resolution to Gb (homotonic relaxion from Dbo) even if it is not a note of the scale (Fig. 15).

A very similar thing could be said from the chord (b) in Fig. 14; in this case its main resolution would be in a chord based upon E, but as we have explained with the Tristan chord, if we apply the different homotonic relaxions between fundamentals, this chord would also have other harmonic relaxions (Fig. 16). The precisest harmonic notation for this chord would have to be with D# instead of Eb (I have put Eb just to show how the convergent decomposition can help to find the melodic enharmonies). This chord, for melodic reasons, can perfectly appear with Eb when the resolution is due to the relaxion of the secondary fundamental on a chord based on D. For ease of understanding of Fig. 16 the same symbols have been used for all the examples, but in cases (a), (c), (d) and (e) it would be more correct to put D#.

Obviously, the resolutions in Fig. 16 are not conclusive; they merely reveal a locally harmonic relaxion5 –in some of them, for example (e), there is sonance tension. I insist, once more, on the importance of distinguishing between harmonic (homotonic) local tensions, the tensions of sonance and the tonal tensions. In this book, only the first group is examined.
In the last chapter it was mentioned that global homotonic relaxion is not exactly the clear result of all homotonic vectors that participate in all directions (in examples (d), (f) and even in (a) there is some homotonic relaxion also in the opposite direction).

In example (b), there is the same lack of relaxion from left to right as there is from right to left. The fundamentals pass through a tonal axis and so there is no relaxion in any direction. It is curious that this example forms a palindromic canon in four parts.
In example (c) we have a continuous homotonic relaxion in only one direction –even if the harmonic progression is ascendent (every two chords) with tonal tension–. We have to insist again on the difference between homotonic and tonal relaxions. As example (c) is comparetively long, the creation of a tonal field is inevitable: in this example every two chords a tonal vector is formed (to E, B, F#) which contrasts with the mere homotonic relaxion. It is clear enough that the descendent melodic lines considerably reinforce the harmonic relaxions. If we interpret the excerpt in the opposite way we would realize that there is local homotonic tension but in a resolutive tonicization process every two chords (to C#, F, B). In this example the fundamentals form a canon at the fifth. In this one and in example (b) all the chords have the same structure to avoid influences of sonance and so they belong to a single chord-mode class.
Chord-mode class tables
Once the meaning of chord-mode class has been explained, we will continue with the chord-mode class tables on pages 56 to 61.
On these tables there are represented all the possible (different) chord-mode classes that could be formed with the equal tempered gamma of 12 tones. They are grouped depending on the number of notes in each chord-mode class. There are 351 but each group is numbered differently.
The representative chosen for each family of chords and scales included in each chord-mode class is the one nearest to the convergent structures of which it is formed. With chord-mode classes of six or more notes it is difficult to say which is the best representative because there are many different possible ways to chose from –specially for chords that can be decomposed in more than two convergent chords–. In these cases, the representative chosen is one of the many possible ones. There are also cases of chord-mode classes that can be decomposed in different ways: in these cases, the representative with the more powerful convergent chord structure is chosen.7
From the groups of seven or more notes, the chord-mode classes are written in scale form. When choosing the representative we have taken into account that the first note is the tonic or most magnetic note of the group (depending on the convergent harmonic chord tendencies and transposing all the group in relation to C). There are a lot of chord-mode classes with different possibilities and in some scales the representative chosen could have been another one.8
In staves where the chord-mode classes are written vertically (up to six notes) our aim has been for each stave to show a large functional family of chords determined by the interval formed between the two most powerful fundamentals. The position of chords show their resemblance or relation according to the convergent structure of other chord-mode classes of the other staves. The vertical dotted line at the end of each group of five and six notes separates the chords that cannot be decomposed as a sum of two convergent chords. For the rest, the two significative convergent chords that form them are expressed as of a fundamental figure which we will explain consecutively.
The way of representing the potency of convergence of the fundamentals is shown in Fig. 4 .
Fundamental figuring
When a chord-mode class can be separated in two convergent chords, its harmonic meaning can be shown when specifying the interval and the potency of their two fundamentals. These fundamentals are situated in two ways depending on their intervalic relationship. If the fundamentals belong to different tonal axis one is subordinated to the other (except one particular case),9 in the sense that considering the fundamentals as harmonic trails, one generates the other. Figuration of the chord-mode class cannot be simplified because the fundamentals are representatives of real notes and not harmonics so they have both to be represented even if one seems the resounding of the other. We do that by establishing the secondary fundamental (subordinate) at the right superior part of the main fundamental, that is: at the top we situate the major thirds, fifths and minor sevenths (the minor ascendent seconds as well even if it is a special case).10 When the two fundamentals belongs to the same tonal axis we will put the fundamentals that form tritone or minor descendent third at the right inferior part. In that case, there is not a fundamental subordinate11, both have the same relationship; the importance of each fundamental will only depend on their convergent potency.
Once the fundamental figure is made, we have:
First (left hand side on page 56): in the six bottom staves, the fundamentals are combinations of C convergent chord structure (seven first harmonics), and
Second (right hand side on page 57): having transposed the main and secondary fundamentals to the same level, the rest of fundamentals configure the three tonal axis.
In this way, we have three different types of notation and consequently, three wide chord areas with harmonically differentiated functions:
1) Chords that have a single fundamental (convergent chords)
2) Chords that have both fundamentals on the same tonal axis. This group is divided into two types according to the interval between fundamentals which can be a minor third or a tritone.
3) Chords that have both fundamentals on different tonal axes. They are divided according to the interval between fundamentals which can be a major third, fifth, minor seventh or minor second (we could also separate the minor second relationship as a particular case).
As a whole, we have seven functional classes distributed in three family types (or four if we consider the minor second as a particular type). (Fig. 18)

Partial fundamentals
For each chord, divisible or not, in two fundamentals, we always specify –in the chord-mode tables– all the other interval structures which can also have convergent meaning (in a dotted line for groups that have less than seven notes). The fact that the interval combination grows exponentially at the same rate as the number of notes (and the convergent components potential meaning decreases) we have used the following criterion to represent (or not) partial fundamentals at the chord-mode tables: (ex. in G)
a) Chord-mode classes with one to five notes: in addition to the fundamental figure, we have also specified (below the dotted line) the fundamentals belonging to the following convergent chords examples (ex. in G):

b) Chord-mode classes of six and seven notes: in addition to the fundamental figure, we have specified only the fundamentals belonging to the following convergent chords examples (ex. in G):

c) Chord-mode classes of eight notes: we have only specified the fundamentals belonging to the following convergent chords examples (ex. in G):
d) Chord-mode classes with nine to twelve notes: we have only indicate the complete convergent chords (ex. in G):

In all partial convergences the fundamental without a fifth is written in a smaller notation.
Reference diagram
From chord-mode classes of seven or more notes –in order to represent this fragmentation of partial fundamentals in a significative harmonic structure–, the partial fundamentals are placed following the reference diagram shown below (it is suggested by the structure of the fundamental figure):

The three horizontal lines of figures show the three tonal axes; vertically they form intervals of a fifth. The fundamentals on each level are always an homotonic relaxion in relation with the fundamentals of the anterior level except for one combination (the 4th. order homotonic relaxion which acts in the opposite direction –see notes on page 18–).
The practical consequences of this diagram are numerous. The application into a chord-mode class makes it easy to find the resting notes and the chords' and scales' stability. In this way, for example, a very useful way to know the tonal tendencies of a chord or scale is to find the intervals of major second of the diagram (which will always be at different levels) –so as this interval provides the functions of dominant and subdominant–. The potency of the fundamentals will also give us some useful information. For the same number of notes, a diagram with many figures will mean that the harmony of the chords is not very stable; a diagram containing only a few figures which show tendency to form columns will develop a more stable harmony. The application of the homotonic relaxions to each fundamental in the diagram gives us theoretically resting points in the scale, we can observe if the relaxion is completed by other fundamentals in the diagram because they have always to be on the lower level, and so on...
For example, if we decompose the Guido D'Arezzo hexachord (11th. century) we will only find two main convergent chords which are C and F (as there are no tritones and they are the only notes to have major thirds). If we apply the homotonic relaxions of 1st, 2nd and 3th order to these two fundamentals we will have the notes D, E, F, G12, that is the finalis of the gregorian Oktoechos modes (protus, deuterus, tritus, tetrardus), the most frequently used modes for five centuries until Glaureanus' Dodecachordon (1547) increased the modes to 12 (6 finalis). This increase in the number of modes was caused by the consolidation of the heptachord –where G<198> appears as a new added fundamental having the relaxions to C (1st. order) and A (3th. order) which would be transformed afterwards into the major and minor modes misplacing completely the others in the musical practice, probably because of the more powerful meaning of this new fundamental (make up by a full convergent chord).
Complementary chord-mode class
If we look at Fig. 12 we will observe that the number of five notes chord classes is the same as the seven notes, that the number of four notes chord classes is the same as the eight, the number of three notes chord classes is equal to the nine and so on. This comes from an unique complementary chord-mode class formed just by the notes that are missing (to complete the scale of 12 tones). The harmonic relationship between a chord and its complementary, that is, the intervalic relations between fundamentals, seems not to have any special rule, if there is it was not possible to find it. We are referring to the global functional harmonies between chords and their complementaries. Obviously, as a chord or as a scale without transposition the relationships are of chromatic tension.
What is the usefulness of chord-mode class tables?
As a final point I would like to add that the main functions of these chord-mode class tables is not as a tool for composition or harmonic analysis but to aid understanding of the internal harmonic constitution of chords and their scales and its importance with respect to inter-chord communication. And added advantage is having the billions of chords and scales functionally summarised in 351 chord-modes classes on only six pages. All that thanks to the emulation, applied to timbred notes, of the process of audition as the convergence of a group of pure sounds in two concepts which are not naturally separated: that's of pitch and timbre.
In practice what is really useful to know is how to find the fundamental figure for a chord-mode class or its more powerful fundamentals by the convergence of chords. This could be done by using these tables or not, depending on the complexity of the chord-mode class and the experience in that practice. In the first appendix we will show the easiest way to find the convergencies of any chord or scale, using or not the tables.
CHORD-MODE CLASS TABLES
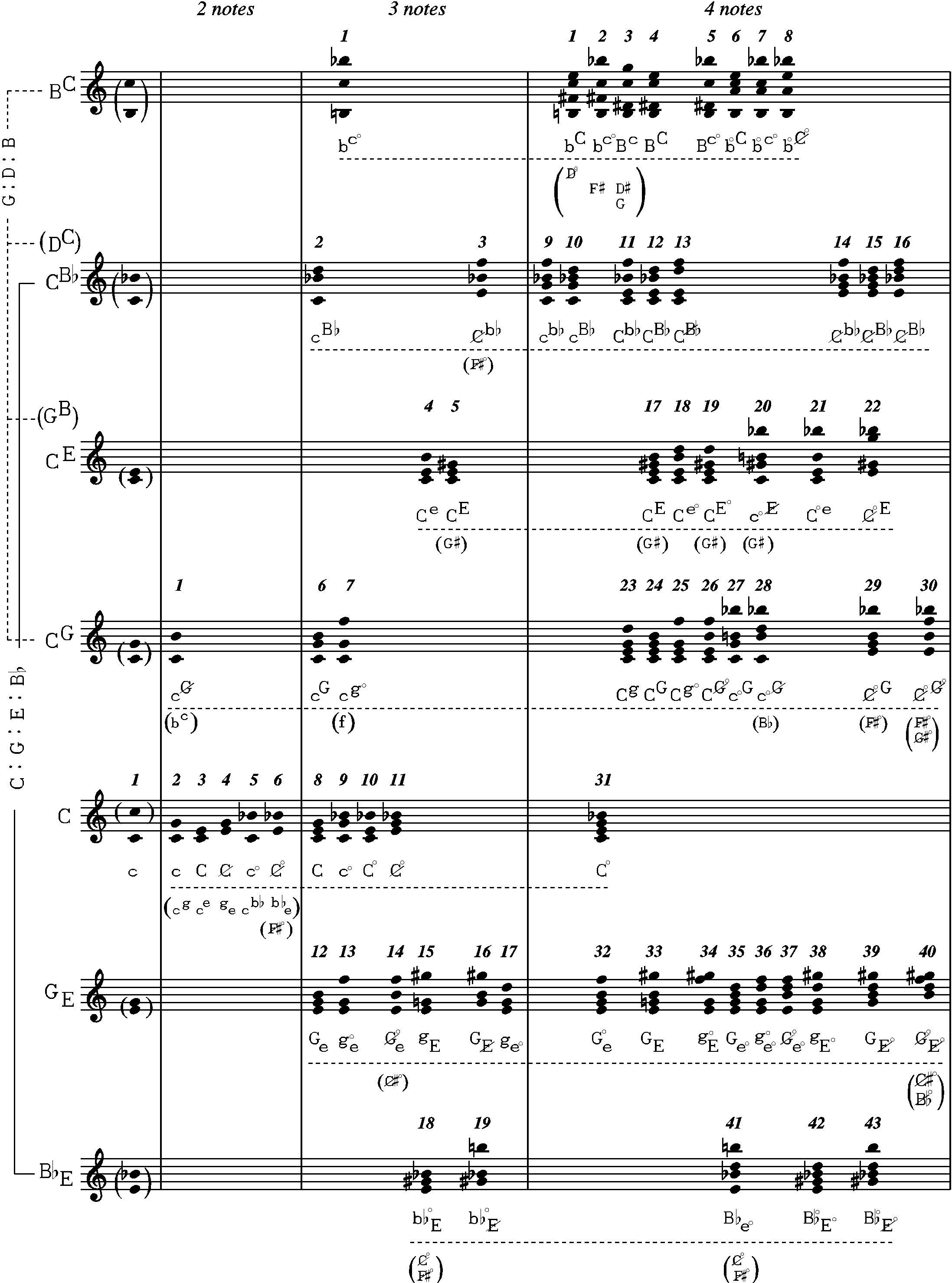





(1) They are the ones classified numerically in table 3 appendix 1
(2) Except the cases of double cycled scaling (cyclical modes). See appendix 3
(4) Table 8, appendix 4 shows the relation between chord-mode classes and PC-Set
(5) If we play the examples in Fig. 16 continuosly on the piano there is a risk of creating a tonal field towards E which would interfere with the local homotonic relaxion we want to demonstrate.
(6) The theory of grades can analyse fragment (a) in different ways: first, as a cadential ¨6:4 in A minor resting on the dominant, that is, situating the resting in E major, secondly as I-V-I cadence in A minor with the resting in A minor chord and even as a I-IV-I plagal cadence in E major resting in this chord. All the explanations would be corect. In fact, the best would be to say that all three happen at the same time.
(7) See Fig 4. The other partial convergent chords however are always specified in the tables.
(8) Although the process has been done with the help of a computer the election of a representative consisted in choosing one of the alternatives proposed by the computer which I personally had programmed. Think that there are, for example, 55.440 possible chord-mode representatives of six notes and 1.663.200 for eight notes.
(9) It is the case of the minor second, as we will see.
(10) We put in this position to follow the logic of the tonal axes. as we will see.
(11) An extreme case would be to refer these two fundamentals to a hypothetical convergence into a virtual fundamental of fundamentals. For example, to refer the fundamentals G and E to a primigenial C.
(12) Relaxions in the same hexachord. There are of course other relaxions outside this scale.